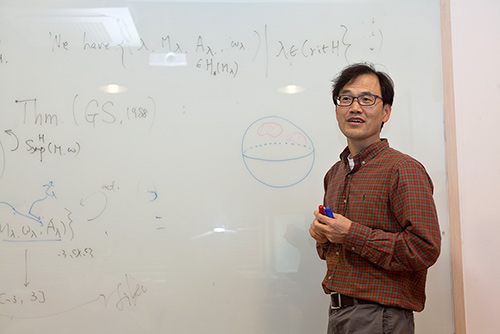 뉴스센터
뉴스센터
| 제목 | '사교위상수학과 플로어 상동성' 분야의 기본 교과서 출간 | ||||
|---|---|---|---|---|---|
| 작성자 | 대외협력실 | 등록일 | 2015-11-13 | 조회 | 5415 |
| 첨부 |
 thumbp1.jpg
thumbp1.jpg
|
||||
|
'사교위상수학과 플로어 상동성' 분야의 기본 교과서 출간. - IBS 기하학 수리물리 연구단 오용근 연구단장 -
여느 연구실과 달리 편안한 분위기가 느껴졌다. IBS 기하학 수리물리 연구단 단장인 오용근 포스텍 수학과 교수의 연구실에 들어섰을 때 받은 첫인상이었다. 오 단장은 지난 9월 영국 케임브리지대학 출판사에서 《사교위상수학과 플로어 상동성(Symplectic Topology and Floer Homology)》이란 책을 출간했다. 총 2권으로 구성된 이 책은 사교위상수학과 플로어 상동성 분야에 입문하는 학자 또는 학생에게 유용한 교과서가 될 것이라는 평가를 받고 있다. 오 단장을 만나 책을 집필한 계기와 그 내용을 들어봤다. 대학원생 시절의 애로점을 해결하다 그는 서울대 재학 시절 기하학에 관심을 갖기 시작해 UC 버클리로 유학을 떠난 뒤부터 사교기하학(symplectic geometry)을 연구하게 됐다. 1983년 그가 대학원에 다닐 때 러시아 수학자 미하일 그로모프(Mikhail Gromov)가 사교기하학 분야에서 굉장히 기념비적인 논문을 발표했다. 덕분에 이 분야는 지난 20년간 비약적으로 발전했다.
"대학원생 시절 사교기하학 분야를 공부할 때 많은 애로점이 있었습니다. 체계적으로 설명해주는 '소스(source)'가 없어서, 논문 자체를 읽고 스스로 터득해야 했기 때문이죠. 이 분야를 연구한 지 20년이 지났지만, 아직도 이 분야에 입문하는 학생들은 공부하기 어렵지요." 이번에 책을 집필하고 출판한 계기도 오 단장의 경험과 맞닿아 있다. 오 단장은 "이 책은 대학원생, 갓 시작한 포스닥(Post-Doc)을 겨냥해서 이 분야의 교과서로 생각하며 10여 년간 집필한 성과"라고 밝혔다. 그는 위스콘신대학에서 20년간 재직한 뒤 2년 전에 IBS에 합류했는데, 2002년~2005년 사이에 강의한 내용을 종합해서 집필을 시작했고 IBS에 와서 집중적으로 마무리할 수 있었다고 한다. 오 단장은 "2009년 일본 수학자들과 함께 이 분야에 대해 쓴 책이 있지만, 구체적인 예시 없이 일반적인 이론을 다뤘기 때문에 훨씬 복잡해 대학원생이나 포스닥이 읽기 어려웠다"며 "이번에 혼자서 쓴 책은 사교위상수학의 문제와 해결 방법을 전체적으로 제시한다"고 강조했다. 특히 이번에 출간된 책에서는 사교위상수학의 문제를 해결하기 위한 도구로서 '플로어 상동성'을 다뤘는데, 이 도구를 습득하려면 해석학, 기하학, 대수학 등 수학적 지식이 많이 필요해 종합적으로 설명했다고 한다. ‘플로어 상동성’이란 ‘양자적 상동성’? 기하학은 굽은 정도, 구부러지지 않는 성질 등을 연구하고, 위상수학은 연속적으로 움직이는 운동에 대해 변하지 않는 양을 다룬다. 도넛을 예로 들면 기하학은 도넛의 굽은 모양을 연구하지만, 위상수학은 도넛의 구멍이 하나라는 사실이 연속적으로 움직일 때는 변하지 않는 다는 것에 주목한다. 사교기하학과 사교위상수학을 이해하기 위해서는 물체의 움직임을 다루는 고전역학인 해밀턴역학에서 출발해야 한다. 오 단장의 설명에 따르면, 해밀턴역학의 기본요소를 추상화하여, 수학적 공간인 다양체로 일반화한 것이 사교다양체(symplectic manifold)이고, 이런 공간의 성질을 연구하는 분야가 사교기하학 또는 사교위상수학이다. 해밀턴역학의 기본요소를 추상화하는 예로는 위치-속도 공간의 넓이를 보존하는 것이 있다. 오 단장은 "수학자들은 기하학적인 구조의 성질을 파악하기 위해 온갖 도구를 도입하는데, 사교다양체는 굉장히 난해하고 미묘해서 그 성질을 알아내기 위해서는 대단히 복잡하고 아주 세밀한 해석학적인 도구가 필요하다"며 "그것을 도입한 수학자가 바로 그로모프"라고 설명했다. 우주공간의 성질을 찾으려면 우주선을 보내서 데이터를 얻듯이 수학자들은 다양체 위에서 그 안에 들어 있는 '부분 다양체'를 생각한 뒤 그것을 움직여서 동역학적인 상호작용을 살펴본다. 이렇게 동역학과 부분 다양체의 상호관계를 관찰함으로써 그 바깥 공간의 성질을 유추할 수 있는데, 이를 위한 대수적 방법론 중 하나가 바로 사교기하학에서의 플로어 상동성이다. 플로어 상동성은 1980년대 말 독일 수학자 안드레아스 플로어(Andreas Floer)가 미국 뉴욕주립대에서 포스닥을 하면서 그로모프 이론을 해밀턴역학과 결합시켜 만든 개념이다. 플로어는 '아놀드 추측'을 해결하기 위해 이 개념을 창안했다. 소련 수학자 아놀드가 1960년대 중반 재창한 이 가설은 사교공간에 있는 해밀턴 흐름에서는 반드시 몇 개의 주기점이 있어야 하는데, 그 수가 적어도 사교다양체의 상동성의 개수만큼 있어야 한다는 내용이다. 예를 들어 주기점은 물이 자유롭게 흐르는 호수에 종이배를 띄웠을 때 1시간 후에 정확하게 제자리로 돌아오게 되는 지점이라고 할 수 있는데, 이런 주기점의 개수가 호수의 상동성의 개수보다 더 많다는 뜻이다.
그렇다면 고전적 상동성(homology)과 플로어 상동성은 어떻게 다를까. 고전적 상동성이란 공간의 가장 중요한 위상적 정보로, 예를 들어 평면, 구면, 도넛의 차이점을 수학적으로 구별하는 기본적 방법을 제시한다. 한 예로, 구면 위에 있는 임의의 원은 연속적으로 줄여서 한 점으로 만들 수 있지만, 도넛 위에서 구멍을 한 바퀴 도는 원은 이렇게 할 수 없다. 이런 구멍의 존재가 상동성의 원소로 기록된다. 오 단장의 설명에 따르면, 플로어 상동성은 주기 궤적들과, 궤적들을 연결하는 원통형 복소 곡면을 사용해 정의되는 불변량이다. 기존의 상동성은 에너지 레벨을 0으로 가지며, 플로어 상동성은 이를 모든 에너지 레벨로 확장하는 것으로 이해할 수 있다. 이런 의미에서 플로어 상동성은 '양자적 상동성'이라 불리기도 한다. 사교기하학과 복소기하학은 거울대칭 오 단장은 "플로어가 아놀드 가설을 해결하기 위해 플로어 상동성을 창안했지만, 지금은 플로어 상동성이 사교위상수학을 연구하는 근본적인 도구로 자리를 잡았다"며 "내 자신도 이에 대한 나름의 믿음을 갖고 포스닥 시절부터 지금까지 계속 플로어 상동성을 사교위상수학의 다른 문제에 적용하기 위한 연구를 해오고 있다"고 말했다. 1990년대 중반 오 단장은 영국 케임브리지대 뉴턴연구소에서 한 학기 동안 방문연구원으로 있으면서 플로어 상동성을 아놀드 추측 이외에 사교위상수학의 다른 문제를 해결하는 데 최초로 성공했다. 또한 추상적으로 정의된 플로어 상동성을 통해 '플로어 스펙트럼 불변량(Floer spectral invariant)'이란 구체적인 불변량을 유추해내는 일을 했다. 오 단장은 2006년 스페인 마드리드 국제수학자대회에서 초청연사로 초청받아 플로어 상동성을 사교위상수학의 여러 문제에 적용하고 새로운 방법론을 도입한 업적에 대해 강의했다. 한편, 사교기하학에서 사교는 일본 수학자들이 번역한 단어다. 사교에 해당하는 영문 심플렉틱(symplectic)은 그리스어와 인도-유럽어의 접미사를 결합해서 만든 신조어로 '복잡한'이란 뜻이다. 20세기 초 관련 학자들이 complex geometry라고 명명하려고 했지만, 이미 복소수를 기반으로 한 복소기하학(complex geometry)이 있었기 때문에 새로운 용어를 만든 것이다. 흥미롭게도 필즈상을 수상한 러시아 수학자 막심 콘체비치(Maxim Kontsevich)의 상동적 거울대칭이론(homological mirror symmetry) 제안에 따르면, 생긴 것이 전혀 다른 복소기하학과 사교기하학은 거울대칭성을 이뤄야 한다. 어떤 문제가 한쪽의 관점에서 굉장히 어렵지만, 다른 쪽의 관점에서는 굉장히 쉬울 수가 있어 문제 해결 가능성이 높아질 수 있다는 뜻이다. 특히 사교기하학은 이론물리 분야에서 초끈이론과 상호작용이 활발하다. 예를 들어 그로모프가 사교다양체를 연구할 수 있는 탐사체(probe)가 초끈이론학자 에드워드 위튼의 비선형 시그마모델(nonlinear sigma model)에서 다루는 대상과 실제로 동일하다는 사실을 알게 됐는데, 이로써 1990년대 초 그로모프-위튼 이론이 만들어졌다. 현재 사교위상수학과 초끈이론은 상호 간에 도움을 주고받으며 발전하는 단계에 와 있다. 오 단장은 "사교기하학과 복소기하학도 서로 거울대칭을 이루니까 상호 간에 교류가 활발하다"며 "우리 연구단이 지향하는 연구의 방향과 주제도 바로 이런 것"이라고 설명했다. 예를 들어 한쪽 관점에서 풀리지 않는 문제를, 거울대칭을 이루는 다른 쪽 관점에서 접근해 해결할 가능성을 모색하는 식이다. 플로어 상동성을 좀 더 쓰기 쉽게 만드는 역할의 연구를 했던 오 단장이 이번에 사교위상수학과 플로어 상동성 분야의 기본 교과서를 집필했다는 것은 어찌 보면 당연한 일이다.
|
|||||
| 다음 | |
|---|---|
| 이전 |
- 콘텐츠담당자
- :
- 최종수정일 2023-11-28 14:20