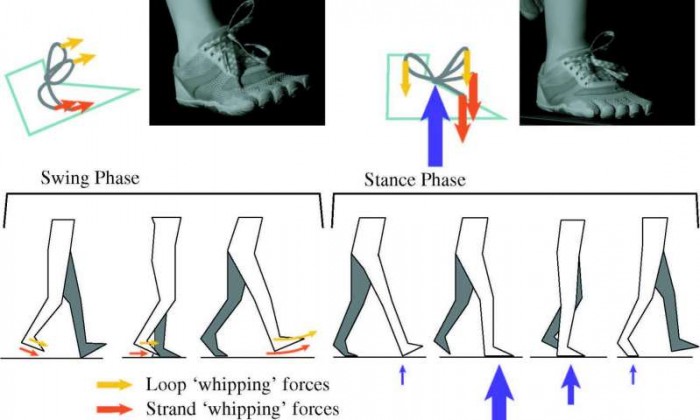
단단히 묶어도 어느 순간 ‘툭’ 풀려버리는 신발 끈. 루프, 이중매듭 등 사람들은 저마다의 신발 끈 묶는 공식을 만들곤 한다. 하지만 이리저리 궁리해도 스르륵 풀려버리는 탓에 신발 끈을 고정하는 ‘슈클립’이 등장하기도 했다. 누가 잡아당기는 것도 아닌데, 왜 내 신발 끈은 자꾸 풀릴까.

초당 900번, 끈 풀리는 과정 촬영해 보니

2016년 신발 끈을 푸는 범인이 마침내 검거됐다. 올리버 오레일리 미국 캘리포니아 버클리대(UC버클리) 교수팀은 제 아무리 단단하게 맨 신발 끈도 끝내 풀어버리는 ‘보이지 않는 손’을 발견한 것이다.
연구팀은 끈이 달린 운동화를 신고 트레드밀(러닝머신) 위를 달리는 사람의 모습을 초당 900번 씩 촬영했다. 이후 촬영된 사진을 느리게 재생하며 사람의 뛰는 행동과 매듭의 연관성을 분석한 결과, 사람이 발을 땅에 내딛는 순간에 신발 매듭이 느슨해진다는 점을 확인했다. 분석 결과, 이는 발을 내디딜 때 받는 ‘중력’과 다리를 앞뒤로 움직일 때 발생하는 ‘관성력’ 때문인 것으로 나타났다.

발을 땅에 딛는 순간엔 중력의 7배에 달하는 매우 큰 힘이 매듭에 작용해 느슨해졌다. 또 걷거나 뛰며 다리를 앞뒤로 흔들면 자신의 운동 상태를 지속하려는 관성으로 인해 매듭 가장자리가 바깥으로 더 당겨지면서 결국엔 신발 끈이 풀리게 되는 것. 걷는 동안 헐거워지고, 잡아당겨지는 것을 반복하다 보니 제 아무리 단단하게 묶은 매듭이라도 결국엔 풀릴 수밖에 없다는 것이다.

▲ 트레드밀(러닝머신)을 달리는 동안 신발 끈이 풀리는 모습을 슈퍼 슬로우 모션 기법으로 촬영한 모습.
오레일리 교수팀은 두 개의 강한 힘이 매듭에 작용하는 것을 포착했다.
(사진 : UC 버클리, 영국왕립학회보A)

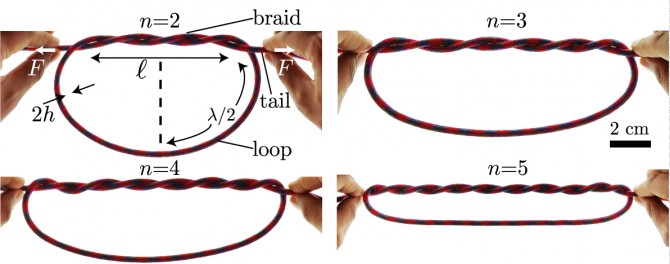
수학이 설명하는 '매듭의 법칙'

중력과 관성력이 철벽같은 매듭도 풀어버린다는 비보에 슬퍼하긴 이르다. 수학자들은 줄을 꼬아 만들 수 있는 다양한 경우의 수를 고려해 절대 매듭을 찾아내고 있다. 2015년 페드로 레이스 미국 매사츄세츠공대(MIT) 도시공학과 교수팀은 줄을 꼬는 횟수와 매듭의 단단함의 관계를 수학적으로 계산한 연구결과를 냈다.

보통 우리가 사용하는 매듭은 동그랗게 고리를 만든 다음, 한쪽 끝을 집어넣고 잡아당겨 만드는 형태의 ‘옭매듭’이다. 연구팀은 이때 줄을 꼬는 횟수가 늘어날수록 매듭이 잘 풀리지 않는다는 점을 수학적으로 계산했다. 연구팀은 줄을 꼬는 횟수를 늘려가며 매듭을 만든 후, 이를 잡아당길 때 드는 힘을 측정했다. 그 결과, 매듭의 힘은 줄을 한 번 묶었을 때보다 10번 묶었을 때 1000배가 세졌다.

이후 연구팀은 줄의 재질, 지름, 탄력 그리고 줄이 꼬인 횟수에 따라 얼마나 매듭이 단단해지는지 계산할 수 있는 일명 ‘매듭의 법칙’을 만들었다. 신발 끈의 풀림은 결국 매듭을 움켜잡는 중심부의 힘과 끝부분을 당기는 중력, 관성력의 힘겨루기에 의해 결정된다. 두 힘의 크기가 계속 같거나 또는 함께 작용하지 않는다면 신발 끈은 절대 풀리지 않게 된다. 여러 번 꼬아 더 묶기 힘든 매듭일수록 더 강력해진다는 의미다.

▲ 일상생활에서 가장 많이 사용하는 ‘옭매듭(Overhand Knot)’은 동그랗게 고리를 만들고 한쪽 끝을 꼬아서 잡아당기기만 하면 만들어진다. 이때 줄을 더 많이 꼬면 묶을 때 힘이 드는 대신 잘 풀리지 않는다.
(사진 : MIT/Physical Review Letters)

넥타이를 매는 17만 가지 방법

신발 끈뿐만이 아니다. 매듭을 묶는 일상적인 일에 수학자들은 ‘엄근진(엄격, 근엄, 진지)’하게 또 다른 공식을 만들었다. 바로 넥타이를 묶는 경우의 수를 계산한 것이다. 매듭 묶기 레벨로 봤을 때 넥타이는 신발 끈보다 한수 위다. 더 복잡한 절차가 있을 뿐 아니라 저마다의 스타일에 따라 다양한 방법을 활용하기도 한다.

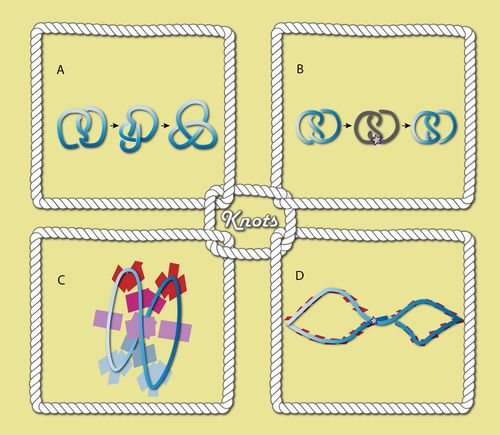
2014년 스웨덴 왕립기술원의 수학자인 미카엘 베데모 요한슨 연구팀이 놀라운 결과를 발표했다. 넥타이 매듭을 묶는 총 경우의 수가 무려 17만7147가지라는 것이다. 모든 방법을 활용하려면 485년 동안 매일 다른 방식으로 넥타이를 매야 한다.

이 경우의 수를 계산하기 위해 연구진은 넥타이 매는 방법을 몇 가지 경우로 나눠 유형화했다. 넥타이를 감는 패턴을 시계 방향, 반시계 방향, 아래서 위로 넣기 등으로 세분화한 결과 유형만 총 2046개를 발견했다. 이후 컴퓨터 프로그램에 매듭의 위치, 개수, 모양 등의 요소를 대입한 결과, 17만7148가지라는 놀라운 결과를 얻은 것이다.

매듭 연구의 시작 : 같은 듯 다른 매듭 찾기

이쯤 되면 ‘그저 매듭일 뿐인데, 왜 이렇게 진지하게 달려들까?’라는 생각이 들기도 할 터. 수학적으로 매듭은 3차원 공간 안에 놓인 한 줄의 상태를 말한다. 우리에겐 일상일지라도 수학자들에겐 연구대상으로 자리매김한 지 오래다. 특히 도형이나 공간의 모양, 성질을 연구하는 위상기하학 분야에서 매듭은 조금 더 특별하다. 다양한 매듭을 구분하고, 이들의 변형을 연구하는 ‘매듭 이론’이란 학문 분야도 있을 정도다.

기하학 연구에서 매듭 이론의 목적은 두 가지다. 첫째로는 어떤 매듭과 고리가 있는지를 연구해 그들을 중복 없이 열거하는 것. 두 번째는 두 개의 주어진 매듭이 같은 것인지를 판정하는 것이다. 중복 없이 열거하는 일이 쉽게 느껴질 수도 있지만, 수학자들이 지금까지 파악한 교차점 수가 16개 이하인 매듭은 170만1936가지나 된다. 이들을 서로 구분하는 것이 말처럼 쉽지 않다는 의미다. 달라 보이지만 같고, 같아 보이지만 다른 것이 바로 매듭이다.

▲ 수학자들은 경우의 수를 고려해 동형의 매듭을 ‘매듭표’의 형태로 정리했다.
사진 속 매듭은 수학적으로는 모두 같은 매듭으로 본다.
(사진 : 미국 네브레스카대)

기초과학연구원(IBS) 기하학 수리물리 연구단도 매듭 이론 연구에 나섰다. 김선화, 안병희, 배영진 연구위원은 기존의 방법으로 구분이 어려웠던 ‘르장드르 특이 매듭’을 구별할 수 있는 방법을 개발했다. 르장드르 특이 매듭(LSK‧Legendrian Singular Knots)은 현대 위상기하학자들에게 주목받고 있는 매듭의 종류다.

▲ 매듭의 종류. 단순매듭(A)은 줄을 끊지 않고도 서로의 모습으로 변형시킬 수 있는 매듭으로 수학적으로 동일한 것으로 본다. 특이매듭(B)은 서로 교차하는 부분에서 오른쪽 줄이 엮이는 방향이 서로 다른 형태로, 엮이는 지점을 ‘특이점(☆)’이라 부른다. 르장드르 매듭(C)은 줄이 일정한 평면(네모난 판) 위에 놓이는 형태이며, 르장드르 특이 매듭(D)은 평면 위에 놓이면서도 특이점을 가지는 형태를 말한다.
(사진 : IBS)

연구단은 매듭이 단순매듭인지, 특이매듭인지, 르장드르 매듭인지, 르장드르 특이 매듭인지를 구분할 수 있는 새로운 메커니즘을 고안했다. 그리고 이를 토대로 르장드르 특이 매듭을 만들 수 있는 경우의 수를 계산한 결과, 르장드르 특이 매듭이 단순 매듭이나 르장드르 매듭보다 더 많은 경우의 수를 가지고 있다는 점을 알아냈다.

DNA부터 우주의 비밀까지 풀어낼 열쇠

수학자들의 계산에서 그치는 것이 아니다. 이러한 매듭은 실제로 우리 실생활에 사용되고 있는 것은 물론, 우리가 잘 알지 못하는 비밀을 풀어낼 열쇠로도 활용되고 있다. 간단히는 외과 의사들이 수술 부위를 실로 꿰맬 때 수술 부위 상처를 최소화하면서 상처가 잘 아물도록 하는 매듭을 만든다. 이 역시 ‘부분적으로 연결된 수술용 매듭’을 개발한 수학자들 덕분에 가능해진 일이다.

▲ DNA를 살펴보면 양 끝이 있는 긴 끈 즉 매듭의 모습이 보인다.
(사진:N.R. Cozzarelli/대한수학회)

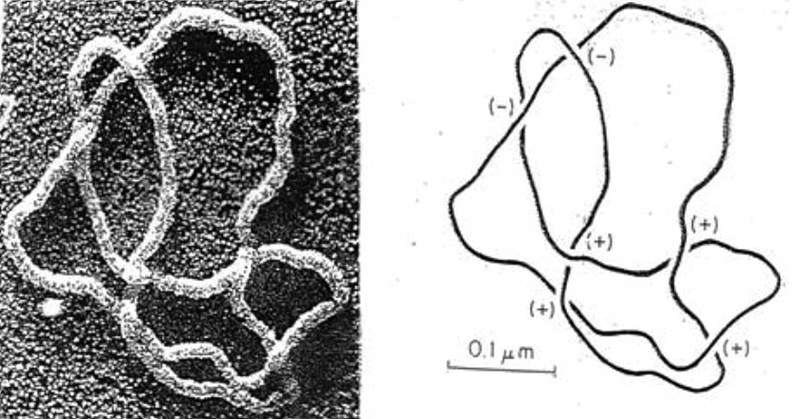
우리 몸의 근간을 이루는 유전자 역시 매듭부터 시작된다. DNA를 살펴보면 양 끝이 있는 긴 끈의 모양으로 평소에는 차지하는 공간을 줄이기 위해 빽빽하게 꼬인 상태로 존재한다. 그러다 유전정보를 복제하거나 단백질을 만들어내야 할 때 잔뜩 꼬인 나선구조를 풀어야 하는데, 효소가 가장 효율적으로 꼬임을 풀 수 있도록 DNA의 적당한 부분을 끊는다. 매듭론은 이 과정을 분석하는 데 매우 요긴하다. 효소가 어떻게 DNA의 특정 지점을 끊었다가 이어주는지에 대한 해답을 주는 것이다.

눈에 보이지 않는 세계 뿐 아니라 거대한 우주에도 매듭이 있다. 은하를 점으로 가정하고 3차원 우주 안에 배치해 보면 흥미롭게도 은하단을 꼭짓점으로 하는 매듭의 모습이 그려진다. 어쩌면 삼라만상의 기본에 매듭이 있다고도 말할 수 있을 터. 그래서인지 수학계의 노벨상이라 불리는 ‘필즈상’ 수상자가 이 분야에서만 여러 명이 나왔다.

이제야 과학자들이 왜 그렇게 각종 매듭을 구분하고 정리하기 위해 수많은 노력을 쏟는지 이해가 될 것 같다. 매듭을 연구하는 과학자들은 수학적 이론을 토대로 세상의 근본의 원리를 탐구하고 있는 것은 아닐까.

본 콘텐츠는 IBS 공식 블로그에 게재되며, blog.naver.com/ibs_official/ 에서 확인하실 수 있습니다.