A fundamental assumption, namely the Born approximation, in the theory of open quantum systems is overcome using statistical mechanics.

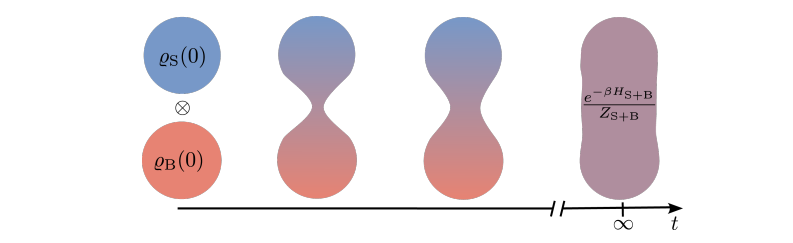
In isolated quantum systems, correlated quantum states are essential for all emerging quantum technologies and have led to the 2022 noble prize in physics. However, in open quantum systems the correlations (quantum or classical) between the system of interest and the reservoir are typically ignored under the Born approximation.

Several attempts have been made to overcome this highly restrictive assumption but a rigorous theory has been lacking. Recently, research team led by Dr. Juzar THINGNA of the Center for Theoretical Physics of Complex Systems (PCS) within the Institute for Basic Science (IBS) presented an approach that allows correlations between the system and reservoir to build over time and correctly accounts for the long-time correlations as dictated by statistical mechanics (cf. illustration).

Their approach uses the long-time highly correlated system-reservoir state (quantum canonical Gibbs state of the system-reservoir composite) and incorporates this knowledge in the dynamical theory resulting in the canonically consistent quantum master equation (CCQME).

Surprisingly, the CCQME drastically improves upon the long-standing issue of unphysical negative probabilities, a common occurrence in approaches that rely on the Born approximation (e.g. Redfield equation).

Using a variety of models, that range from a damped harmonic oscillator to a dissipative spin chain, the group showed that their approach correctly reproduces the correlations built up in the regime of strong system-reservoir coupling. Their theory paves a way to re-investigate nonequilibrium physics in presence of system-reservoir correlations impacting the fields of open quantum systems, quantum transport, and quantum thermodynamics.