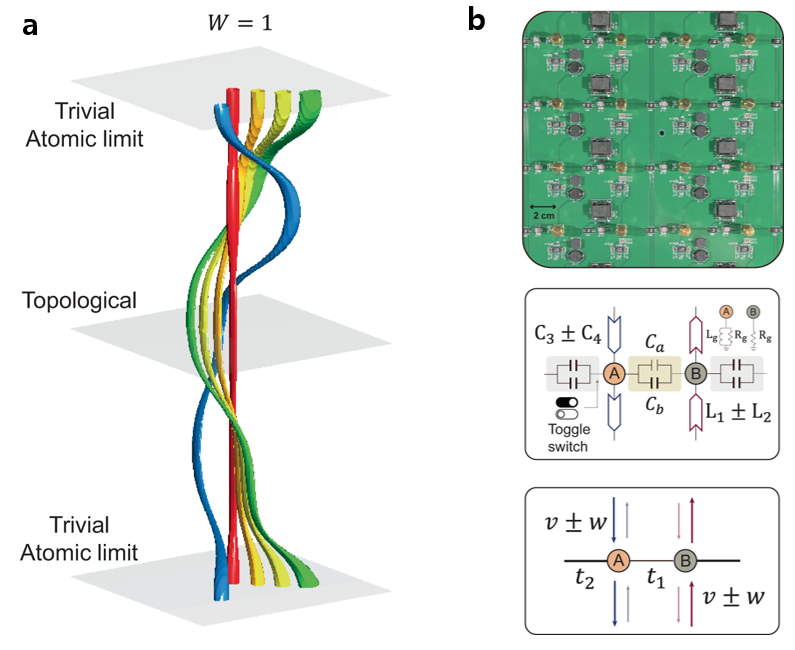
Topology is a branch of mathematics that deals with the geometric properties that remain unchanged under continuous deformations. The number of holes in a torus and the linking of two strings can be examples of topology because these numbers are invariant even if the shapes of the torus and strings change. This abstract field of mathematics is now revolutionizing the understanding of quantum material. Topological matter, whose quantum wavefunction has a non-trivial topological structure, is gathering great interest among physicists as it emerges as a new realm of study where the confluence of mathematics and theoretical physics plays an important role.

The Hopf bundle is one of the complicated mathematical objects that demonstrate the notion of topology, composed of an infinite number of strings mutually linked to each other. The concept of the Hopf bundle has fascinated physicists as it has been one of the challenges in the field of topology, calling for realization in physical systems. However, realization in the real physical world has been challenging due to its intrinsically intricate nature.

In a study published in Communications Physics, a collaborative team led by Dr. PARK Moon Jip and Dr. PARK Hee Chul from the IBS Center for Theoretical Physics of Complex Systems and Prof. Bumki Min from KAIST realized the Hopf bundle in real physical systems composed of networks of electric circuits. These electric circuits not only effectively mimic the motion of electrons inside quantum materials but can also exhibit more intriguing behaviors, such as non-reciprocal coupling. The realization of controllable non-reciprocal coupling is pivotal in the realization of network structures characterized by the non-Hermitian Hopf bundle. The team successfully realized and visually demonstrated the Hopf bundle using these circuit networks.

The discovery of the non-Hermitian Hopf bundle provides a deeper understanding of non-Hermitian topological phases of matter. The authors underscore the possibility of realizing the Hopf bundle in real quantum systems, such as solid-state materials and cold atom systems. If the Hopf bundle could be realized in quantum systems, it would also open up exciting possibilities for utilizing such circuit networks for quantum sensor applications.

Figure 1. a) Experimental demonstration of the Hopf bundles in reciprocal space. b) Photography of the circuit networks.