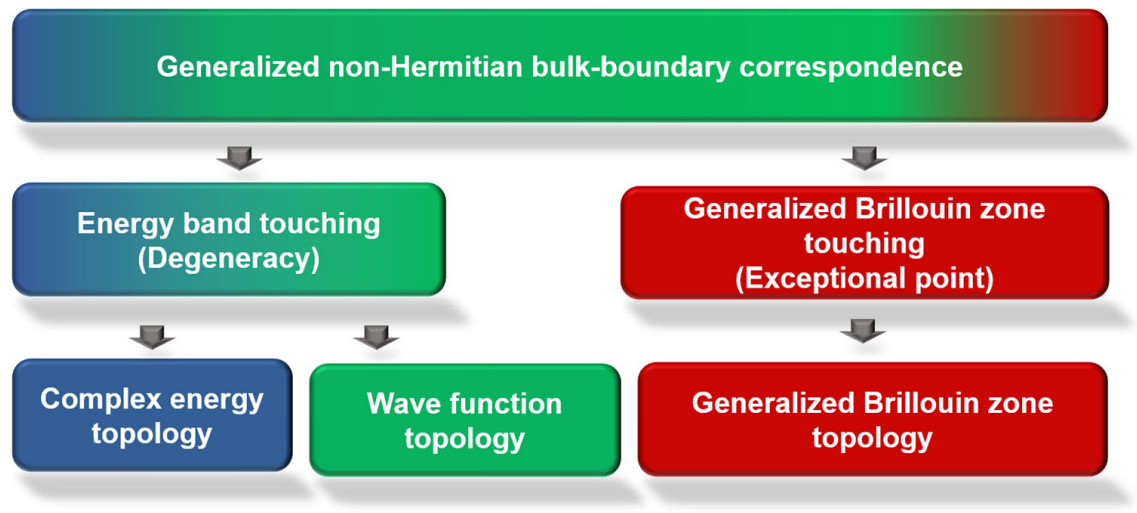
In 1915, German mathematician Emmy NOETHER proposed the seminar theorem of physics, which states that the continuous symmetry of a physical system has a corresponding conservative law of physical quantities. For instance, in a physical system where there is no external time-dependent force (time-translational symmetry), one can define the energy as a good conserved quantity. Similarly, in a uniform physical system where space-translational symmetry exists, the momentum becomes a conserved physical quantity. On the other hand, if we introduce a potential barrier in a system, particles and waves can backscatter. Consequently, the momentum cannot be conserved.

Non-Hermitian physics is a newly emerging branch of physics research that accounts for open or dissipative systems. Unlike the closed system, where the typical physical quantity such as energy, momentum, and particle number are not conserved in the open quantum systems. Non-Hermitian theory of physics resolves such dissipative phenomena by introducing complex valued spectra. For instance, in non-Hermitian theory, the loss and the gain of the particles toward the outer bath can be explained by the imaginary value of the complex energy.

In continuous systems, the physical momentum can be any real-valued quantity. If a physical system is composed of a lattice structure with repetitive periodicity, one can still define the quasi-momentum that has a periodic structure that has topological equivalence with torus. If a physical system completely lacks space-translational symmetry due to potential barriers such as impurity and defect, how would one be able to describe the momentum space?

In a study published in Communications Physics, a collaborative team led by Prof. PARK Moon Jip from Hanyang University and Dr. Sonu VERMA from the IBS Center for Theoretical Physics of Complex Systems constructed the topological theory of generalized Brillouin zone, which describes the complex momentum space in the presence of the translational symmetry-breaking disorder or boundary, The generalized Brillouin zone lives and form an exotic geometric manifold in the complex plane, and it can undergo topological phase transitions that signifies the emergence of the boundary state. The work shows that the bound state due to the potential disorder can be understood as the topological phase transitions of the manifolds of the generalized Brillouin zone.

The theory of generalized Brillouin zone provides a deeper understanding of non-Hermitian topological phases of matter. The authors underscore the possibility that the topological phases in such a generalized Brillouin zone would help to realize new types of robust topological states that are enabled by the openness of the system in addition to the topology that survives in the presence of open systems.

Figure 1. Schematic illustration of non-Hermitian bulk-boundary correspondence in the generalized boundary condition (GBC). In GBCs, generalized Brillouin zones (GBZs) can possess the non-trivial topological invariant, which manifests as the topological boundary mode. These topological boundary modes are not captured in the conventional band topology. The topological phase transition is characterized by the touchings of GBZs, which manifests as exceptional points.